Surface Triangulations and Quivers

Last time I discussed the ADE classification of finite type quivers. I ended that post with a remark that for quivers with relations, there is no classification that is nearly as nice as the ADE classification, in general we work on a case by case basis.  The particular case I am interested is a class of algebras called 2-Calabi-Yau tilted.  These algebras come up in the study of another class of algebras called cluster algebras, we are not going to focus on that connection here instead I want to focus on an alternative construction that uses Riemann surfaces.

By triangulation I mean a diagram like below

Figure 1 : a triangulation of the disc. 

Concretely, a (non-punctured) triangulated surface is a triple $(S,M,T)$ with $S$ is a oriented Riemann surface with boundary, $M\subset \partial S$ a finite set of points in the boundary, and $T$ a maximal collection of non-crossing curves in $S$ with endpoints in $M$.  We will consider the curves in $T$ up to homotopy and we do not make any restrictions on the number of boundary components.

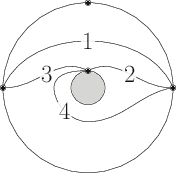Figure 2 : a triangulation of the annulus.

Clearly, we are not dividing the surface into exact triangles, hence, these are also referred to as ideal triangulations.

From such a triangulation we can construct a quiver with relations. We denote this quiver $(Q_T, I_T)$, we take the surface as being understood.  Let the set of vertices be indexed by the arcs in $T$.  There is an arrow $i\to j$ in $Q_T$ if the curves $\gamma_i, \gamma_j\in T$ are incident to each other and form part of the boundary of a triangle $\triangle$ such that $\gamma_j$ follows $\gamma_i$ as you walk around the boundary of $\triangle$ in the counter-clockwise direction (recall that the surfaces are oriented). That definition may seem like a word jumble, so consider the following picture

$\gamma_i$ and $\gamma_j$ are point of the boundary of a triangle and $\gamma_i$ precedes $\gamma_j$, so we get an arrow $i\to j$.

At this point we have only constructed $Q_T$.  The ideal $I_T$ is defined to be the composition of any two arrows that are defined by the same triangle.   It is not obvious from this definition, but there are only three types of triangles in a triangulation

• those with only one edge from $T$, which defines no arrows;
• those with two edges from $T$, which defines exactly one arrow;
• and those with three edges from $T$, which defines three arrows.

Only the last contributes to $I_T$.   The algebra associated to $(Q_T, I_T)$ belongs to a class of algebras called 2-Calabi-Yau tilted. The name comes from the fact that these algebras are associated to certain tilting objects in certain 2-Calabi-Yau categories.  I. Reiten gives a good introduction to the details of which objects and which categories here.

At this point we are ready for examples.  First going back to Figure 1

we get the following quiver

with $I_T = \langle ab, bc, ca\rangle$.  In Figure 2, we hade

which defines the quiver

with $I_T = \langle ab, bc, ca\rangle$.

To clean up the statement of the next theorem, let me introduce one more piece of notation.  Let $\mathcal C$ be the set of all homotopy classes of curves in the interior of $S$ with endpoints in $M$.  The reason for doing this is that the following

Theorem.(BZ) Let $(S,M,T)$ be a triangulation of a surface as given above.  The representations of $(Q_T,I_T)$ are in bijection with $\mathcal C\setminus T$.

The theorem is in fact stronger.  We can define a category with $\mathcal C$ being the objects and morphisms being elementary pivots. Then we actually get an equivalence of categories with the representations of $(Q_T,I_T)$.  I discuss this in detail with additional references here.  The punchline is this, instead of studying the quiver and its corresponding algebra directly, we should be able focus our study on the surface.  For quivers of Dynkin type $A$, which arise as certain triangulations of the disc, this is overkill; but, for other quivers this gives us a new angle to attack their representation theory.  In approximately 2 posts I will give a particular example where the surface presentation is especially useful.

At this point I should mention at least one caveat and 2 possible generalizations of this constructions.  First the caveat.  When defining the arrows, I choose to orient the arrows by traveling the boundary of a triangle in the counter-clockwise direction.  There is no good reason to prefer this direction over clockwise, in fact, many people do use the clockwise direction. Hence, when reading related work using surface triangulations, it is important to look for which convention a person is using.

Now the generalizations.  The simplest generalization is to consider other possible subdivisions of the surface.  Here we required the subdivision to to have 3 boundary segments (at least one from $T$). We can just as easily define $m$-angulations in which the subdivisions have $m$ boundary segments (at least on from $T$).  When the surface is a disc, the resulting algebras are $m$-cluster tilted.

The other possible generalization is to allow the points of $M$ to also belong to the interior of $S$. These surfaces are considered punctured.  The notion of a triangulation must be suitably modified, the details were fully worked out by D. Labardini-Fragoso.  The benefit of the punctured surfaces, beyond having more generality, is that certain triangulations of the punctured disc gives rise to type $D$ quivers. The exceptional Dynkin types $E_6$, $E_7$, and $E_8$ do not occur as triangulations of surfaces.

In the next post I will give an example where the surface realization is used to simplify a calculation.

ADE classification

Last time I introduced the idea of quiver representations, basically, collections of vector spaces and linear maps that are compatible with a given quiver with relations $(Q, I)$.  It turns out that the collection of representations for a fixed quiver  is a Krull-Schmidt category.  This means that we have a notion of direct sums of quiver representations.  It is constructed in the most obvious way, by taking direct sums at each vertex and along the arrows.  For example, it we consider the simple quiver $1 \longrightarrow 2$, then we have the following direct sum of representations

Here I have taken the direct sum at each vertex, producing $\mathbb C^3$, and then identified the last basis element with the the representation $\mathbb C \xrightarrow{1}\mathbb C$.

In practical terms the Krull-Schmidt property means that we can restrict our focus to only the indecomposable representations of $(Q,I)$, those representations that can not be broken into a non-trivial direct sum.   The obvious question is how do I distinguish which representations are indecomposable? In the example given above only the representation $\mathbb C\xrightarrow{1}\mathbb C$.   The larger representation can be broken up into the following direct sum

Where the isomorphism is realized by the pair of matrices $\left(\begin{smallmatrix} 1& i\\0&1\end{smallmatrix}\right)$ and $\left(\begin{smallmatrix} 1& 0\\0&1\end{smallmatrix}\right)$.
(Here I am starting with the original representation and mapping it to the representation with the identity matrix along the arrow.)

The follow up question might be, how many indecomposable representations are there? This question of course requires the question : are there only finitely many indecomposable representations?   Especially as computers get more powerful, the knowledge that there are only finitely many representations would be nice, to identify the indecomposables we would simply need to (get a computer) to enumerate them.   Those algebras that have only finitely many indecomposables are said to be of finite type.

To simplify things I will only consider quivers without relations, that is $I=0$.  With this restriction we get a satisfying though short answer the number questions thanks to P. Gabriel:

Theorem. The path algebra of a quiver has only finitely many indecomposable representations if and only if the underlying graph is a Dynkin diagram of type $A$, $D$, or $E$. 

You may have heard of the Dynkin diagrams before; as the this discussion on MathOverflow shows, they show up in many places across mathematics. The unfortunate result of this theorem is that most quivers will have infinitely many indecomposables.  Of course, the not so unfortunate part is that there is plenty of more mathematics to be done.

So for this restricted case of finite type quivers without relations, how many indecomposables are there?  For type $A_n$ where $n$ is the number of vertices, the indecomposable representations are counted by the $\frac12 n(n+1)$.  For type $D_n$, the number of indecomposables is $n(n-1)$. For types $E_6$, $E_7$, and $E_8$m, the number of indecomposables is 36, 69, and 120 respectively.   In the previous example, that is, $Q$ being $1\longrightarrow2$, there are exactly 3 indecomposables which we can list as
\[\mathbb C\longrightarrow 0,\qquad  \mathbb C\xrightarrow{\ 1\ } \mathbb C,\quad \text{ and } 0 \longrightarrow \mathbb C.\]
I have not said anything about how I generated this  list, that will be a post for a future date.

For quivers with relations the story is much more complicated.  In fact, I don't believe that there is any concise method for determining if an arbitrary quiver with relations is finite representation type. Most work seems to be done in special cases or classes of quivers. Next time I will introduce a class of quivers that are constructed from surface triangulations.  These quivers will not always be finite type, but as a whole have an elegant theory for describing their representations.